티스토리 뷰
그래프 이론의 가장 기본적인 탐색기법인 DFS는 현재 정점과 연결된 다른 정점으로 깊이를 우선하여
탐색하는 알고리즘이다.
간단한 그래프 하나를 예로 들어보자면,

다음과 같은 그래프가 있고 1번 정점에서 탐색을 시작한다고 가정할때
1 >> 2 >> 4 >> 7 >> 8 >> 3 >> 5 >> 6 의 순서로 방문하여 탐색하는것을 말한다.
보다 자세한 과정을 설명하자면 다음과 같이 진행된다.
1. 현재 정점을 스택에 삽입, 방문처리
2. 스택의 top에 해당하는 정점과 연결된 정점중 방문하지 않은 정점 현재 정점으로 취급
3. 1,2 반복수행 >> 현재 연결된 정점들이 모두 방문처리 된경우 스택 pop
4 . 스택이 비워질때 까지 반복수행
이와 같이 스택을 활용하여 깊이 우선 탐색을 진행시킨다.
이때 컴퓨터는 기본적으로 스택구조를 활용하고 있으므로 재귀를 사용한 구현이 가능하다.
이제 위의 예시를 설명한 진행방식으로 그림을 통해 표현해보겠다.

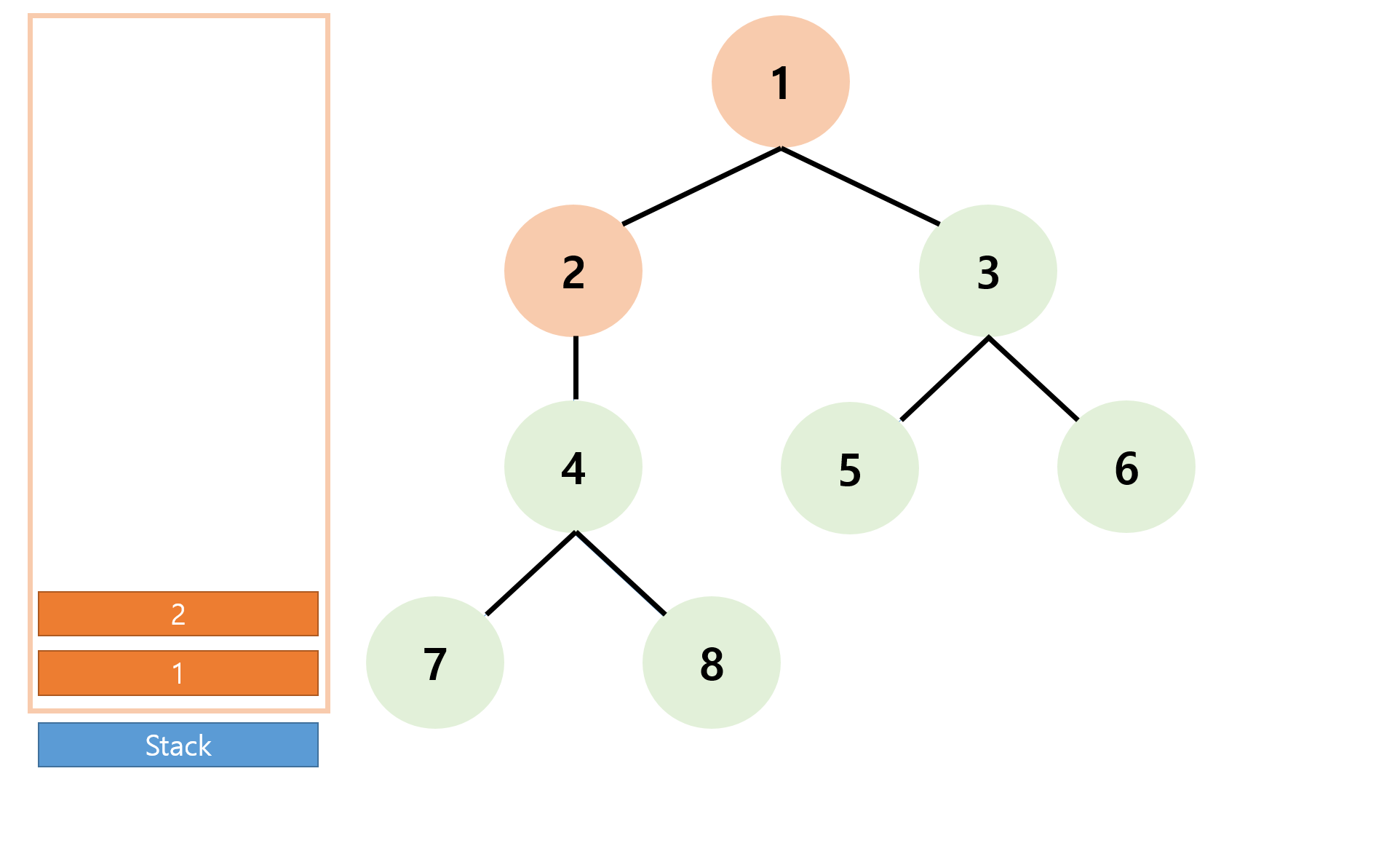
다음과 같은 반복과정을 반복해 정점 7까지 방문 처리된 상황에서 계속 하겠다.
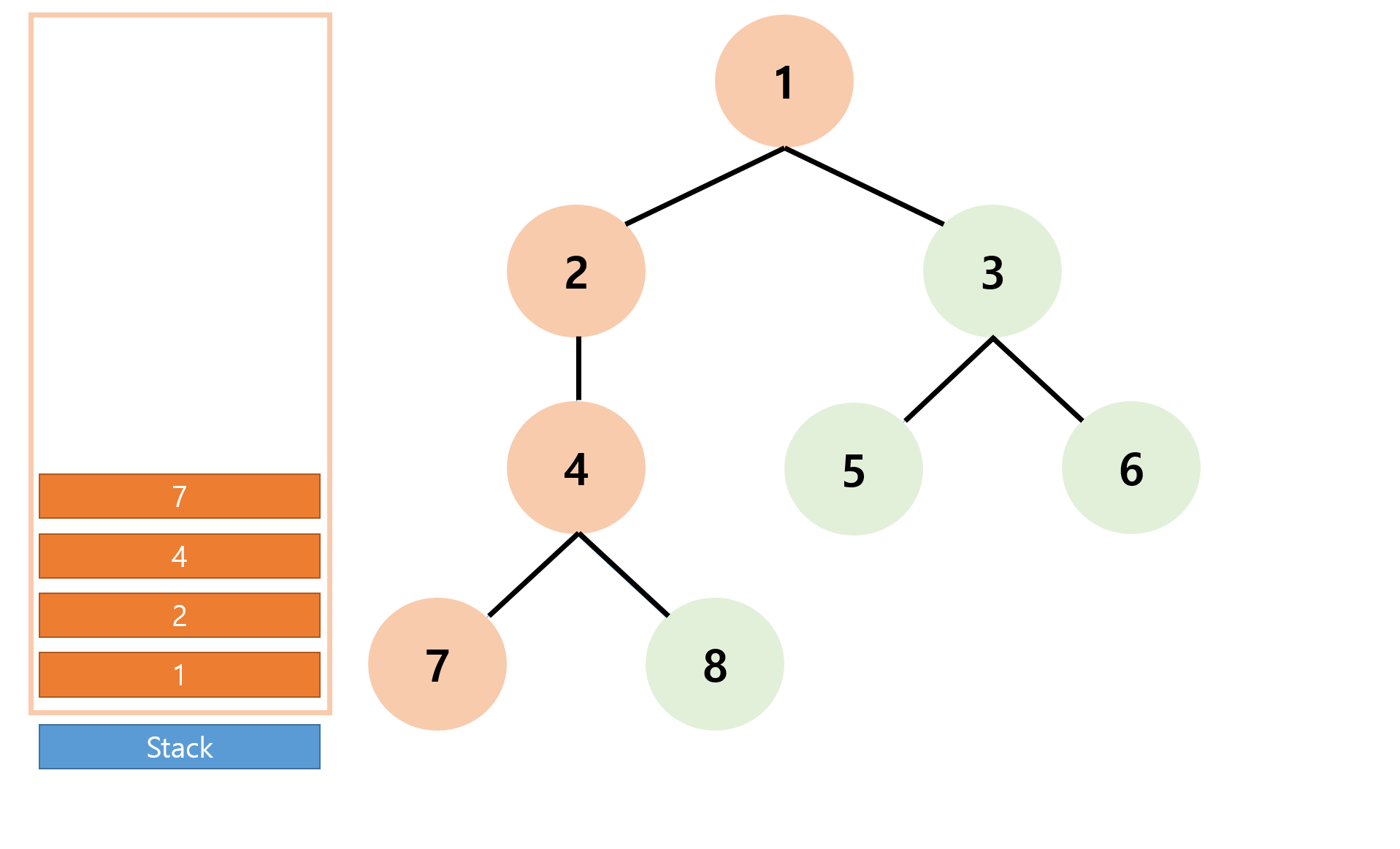
현재 스택의 top인 정점 '7' 에서 더 이상 방문하지 않은 정점이 없으므로 위에서 설명한 진행과정 3을 수행한다.
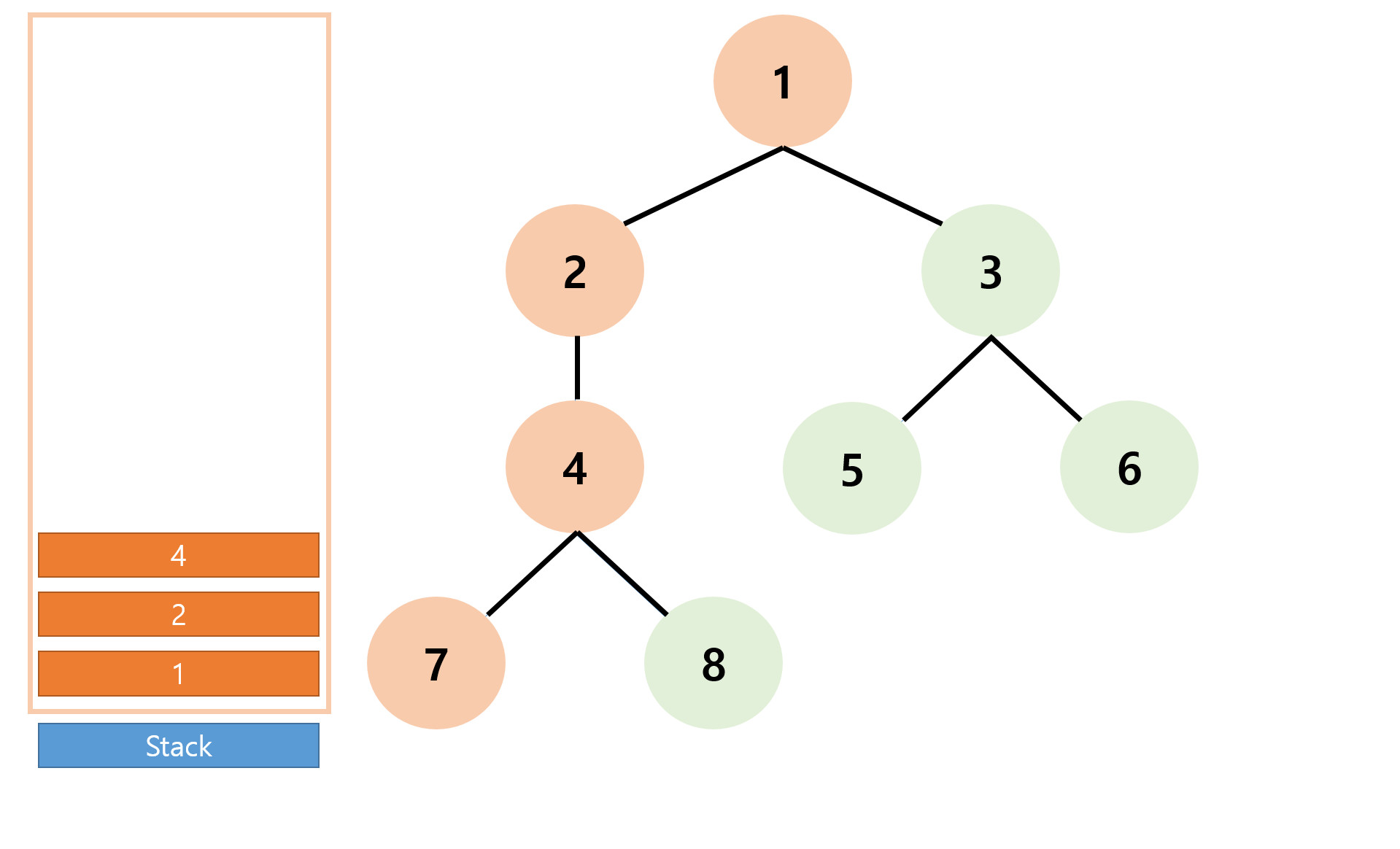
pop 이 진행되어 이제 스택의 top인 정점이 '4' 이므로 다시 방문하지 않은 정점인 '8'로 진행된다.
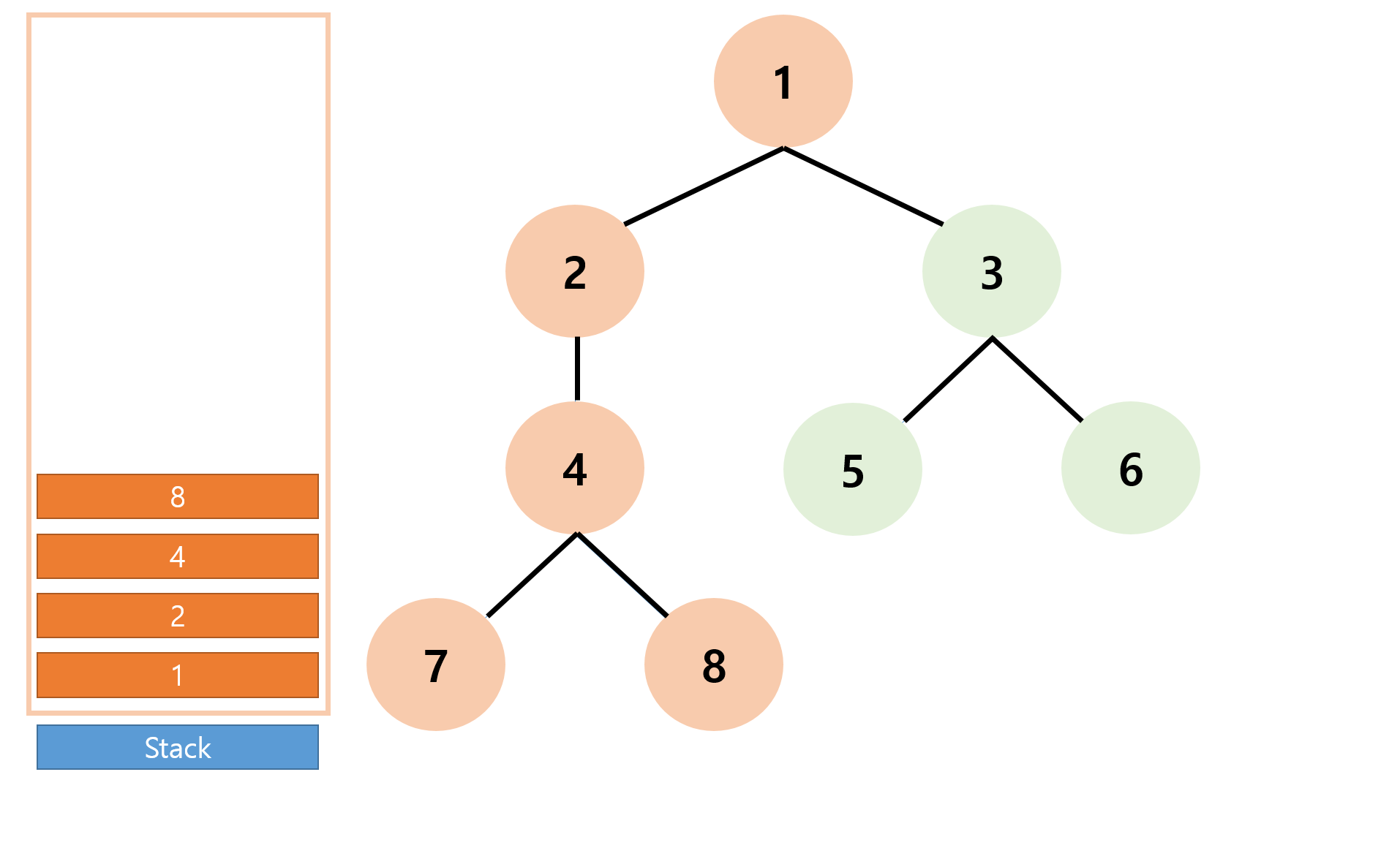
이후 8, 4, 2 모두 더이상 방문하지 않은 정점이 없으므로 연속으로 pop 수행후 현재 스택의 top은 '1'이 된다.
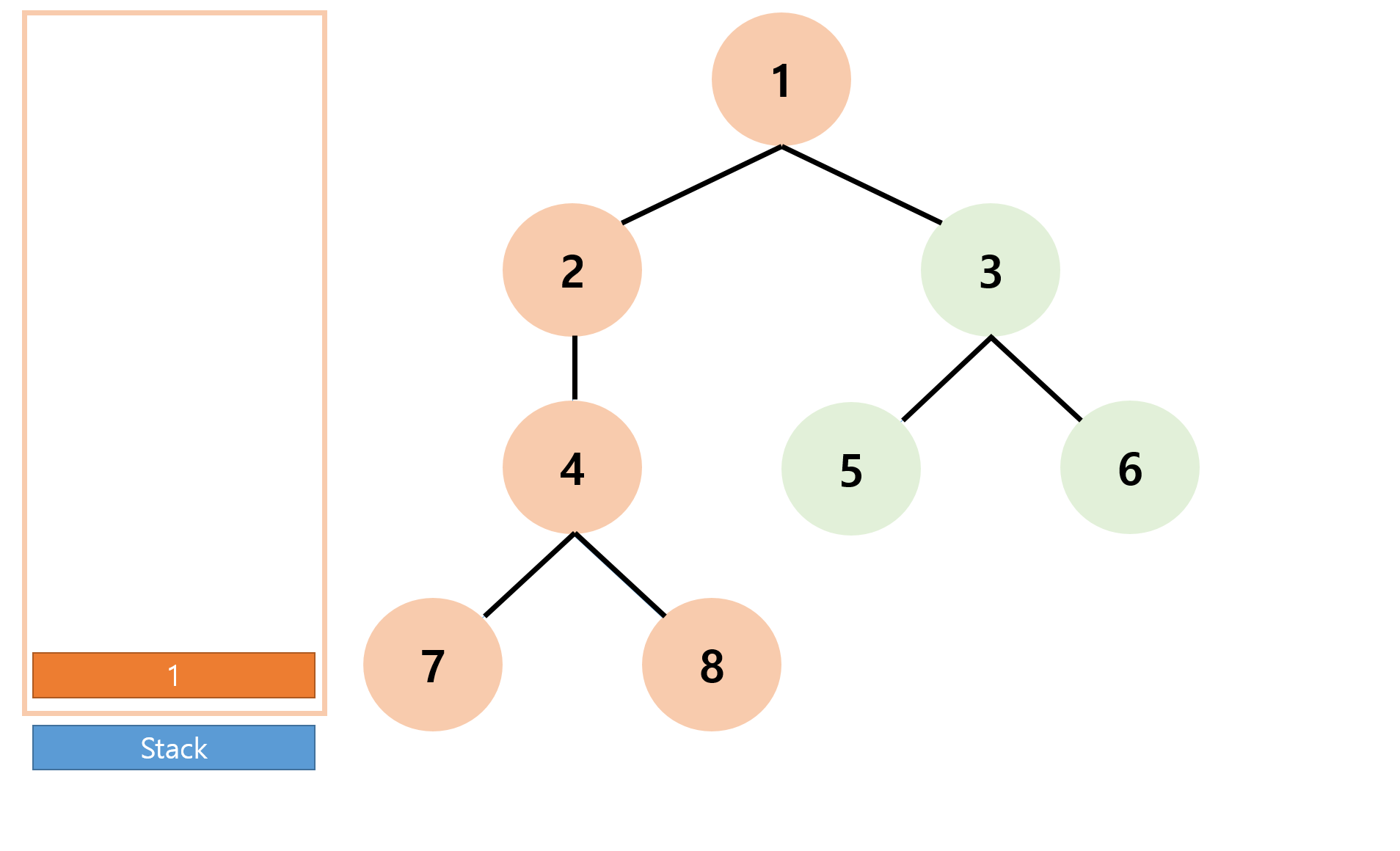
이제 일련의 과정을 다시 반복하면 모든 정점을 방문하게 된다.
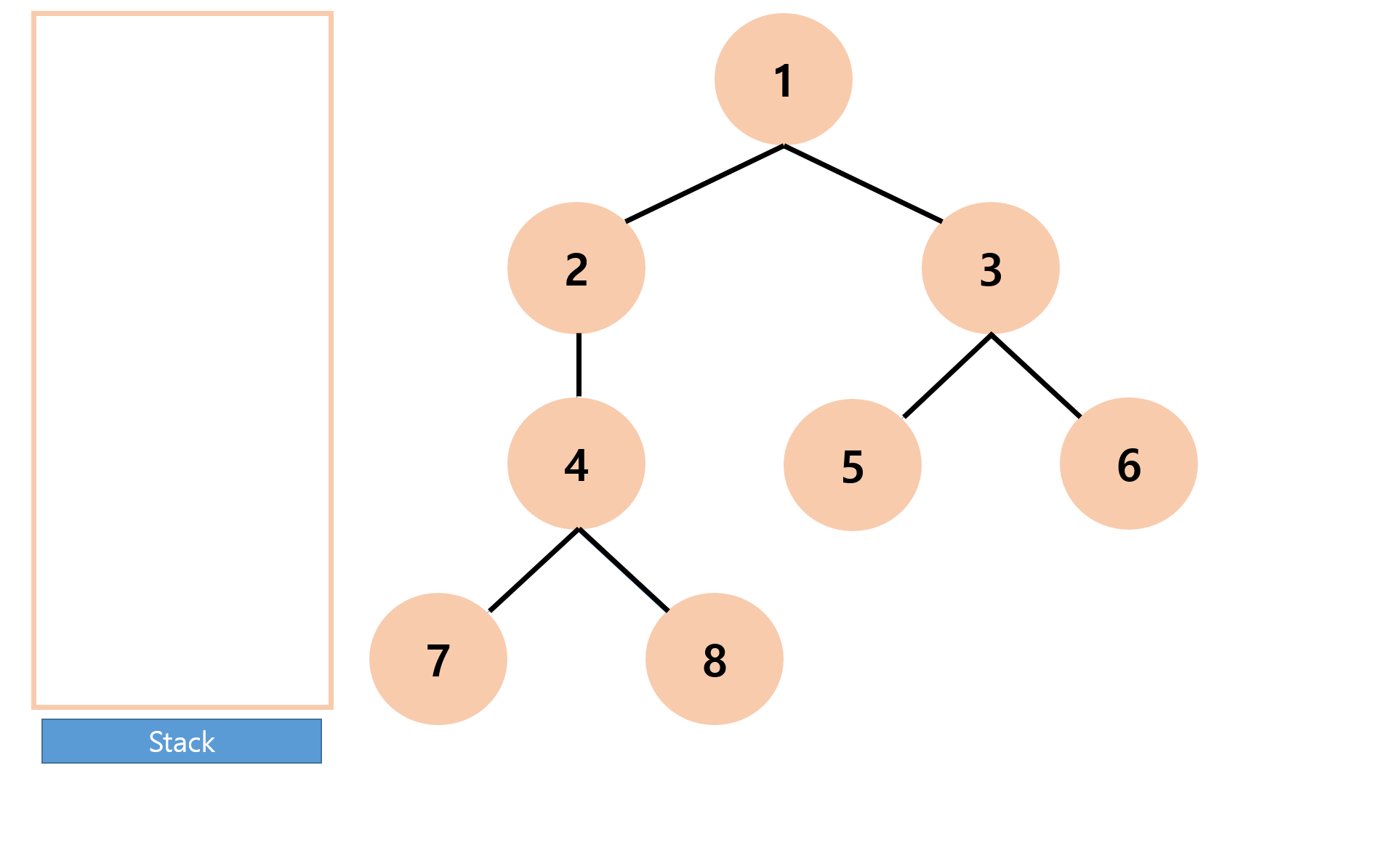
따라서 이와같은 과정을 통해 탐색하는 순서는 1 >> 2 >> 4 >> 7 >> 8 >> 3 >> 5 >> 6 인 것이다.
이제 코드로 구현을 해보도록 하겠다.
우선 연결관계를 저장할 인접행렬, 방문여부에 대한 배열, 그리고 정점의 수에 대한 자원을 멤버변수로 선언하겠다.
private int[][] metrix; // 인접행렬
private boolean[] visit; // 방문여부 확인할 배열
private int n; // 인접행렬 길이
객체가 생성될때 정점의 수를 인자값으로 받아 멤버변수에 자원을 할당할수 있도록
생성자를 선언한다.
이때 직관적으로 볼수 있도록 1부터 n까지 확인할수 있게 길이를 1씩 더 할당해준다.
/**
* 생성자 인접행렬과 방문여부 확인할 배열의 길이를 지정
* @param n : 인접행렬 길이 지정할 정점의 수
*/
DFSImpl(int n){ // 초기화
this.n = n;
this.metrix = new int[n + 1][n + 1];
this.visit = new boolean[n + 1];
}
현재 그래프가 인접행렬로 어떤식으로 표현되는가 확인할 메소드를 선언해준다.
/**
* 인접 행렬 단위 테스트
*/
public void prt() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
System.out.print(metrix[i][j] + " ");
}
System.out.println();
}
}
연결관계인 간선을 입력할 메소드를 선언한다 양방향 그래프이므로 인접행렬에 대칭으로 값이 들어갈수 있도록 한다.
/**
* 현재 그래프의 간선 입력
* @param a : 정점1
* @param b : 정점2
*/
public void init(int a, int b) {
metrix[a][b] = metrix[b][a] = 1;
}
컴퓨터의 기본구조인 스택을 활용하기 위해 dfs 메소드를 재귀로 구현한다.
이때 현재 정점을 인자값으로 받도록 한다.
/**
* dfs 완전 탐색
* @param node : 탐색 시작할 노드
*/
public void dfs(int node) {
if(visit[node]) return; // 방문했다면 pop
visit[node] = true; // 방문처리
System.out.print(node + " "); // 현재 정점 출력
for(int i = 1; i <= n; i++) { // 방문하지 않은 정점에 대해 재귀 호출
if(metrix[i][node] == 1 && !visit[i]) {
dfs(i);
}
}
}
이제 위의 그래프에 대한 간선을 입력받아 예상한 순서로 탐색이 진행되는지 테스트 해 보도록 하겠다.
입력)
8 7
1 2
1 3
2 4
3 5
3 6
4 7
4 8
출력)
1 2 4 7 8 3 5 6
실행 결과)
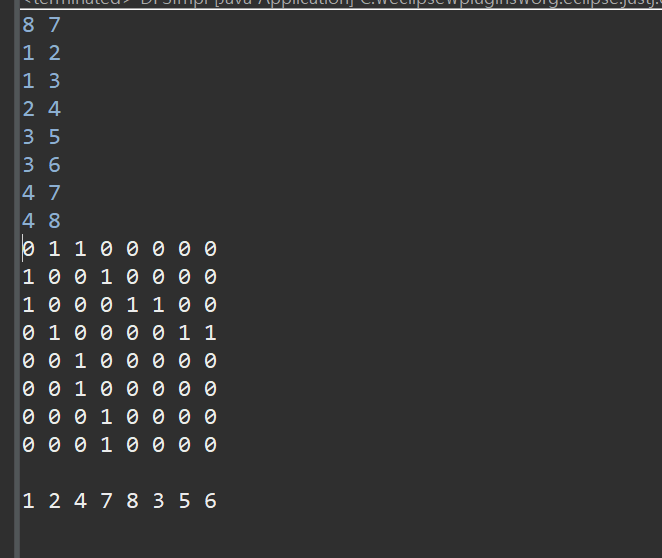
예산한 진행 순서대로 출력되는것을 확인할수 있다.
아래는 코드의 전문이다.
package test;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/**
* dfs 인접행렬 구현
* @author jaewan song
*
*/
public class DFSImpl {
private int[][] metrix; // 인접행렬
private boolean[] visit; // 방문여부 확인할 배열
private int n; // 인접행렬 길이
/**
* 생성자 인접행렬과 방문여부 확인할 배열의 길이를 지정
* @param n : 인접행렬 길이 지정할 정점의 수
*/
DFSImpl(int n){ // 초기화
this.n = n;
this.metrix = new int[n + 1][n + 1];
this.visit = new boolean[n + 1];
}
/**
* 인접 행렬 단위 테스트
*/
public void prt() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
System.out.print(metrix[i][j] + " ");
}
System.out.println();
}
}
/**
* 현재 그래프의 간선 입력
* @param a : 정점1
* @param b : 정점2
*/
public void init(int a, int b) {
metrix[a][b] = metrix[b][a] = 1;
}
/**
* dfs 완전 탐색
* @param node : 탐색 시작할 노드
*/
public void dfs(int node) {
if(visit[node]) return;
visit[node] = true;
System.out.print(node + " ");
for(int i = 1; i <= n; i++) {
if(metrix[i][node] == 1 && !visit[i]) {
dfs(i);
}
}
}
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine()," ");
int n = Integer.parseInt(st.nextToken()); // 정점의 수
int m = Integer.parseInt(st.nextToken()); // 간선의 수
DFSImpl di = new DFSImpl(n);
while(m-- > 0) { // init
st = new StringTokenizer(in.readLine()," ");
di.init(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
}
di.prt(); // 인접행렬 debug
System.out.println();
di.dfs(1); // 완전탐색 결과확인
}
}'알고리즘 > 구현' 카테고리의 다른 글
| 유클리드 호제법(JAVA) (0) | 2023.09.17 |
|---|---|
| [자료구조] 이진 트리와 순회의 구현(JAVA) (1) | 2023.09.16 |
| [자료구조] 큐(Queue)의 구현(JAVA) (0) | 2023.09.13 |
| [자료구조] 스택(Stack) 구현 (JAVA) (0) | 2023.09.12 |
| BFS(너비 우선 탐색) 구현 (JAVA) (0) | 2023.09.04 |
