티스토리 뷰
이번 포스팅에서는 조금 어렵지만 이해하고 사용한다면 정말 강력한 무기가 될 수 있는 힙에 대해 다뤄보도록 하겠다.
먼저 위키백과를 통한 정의를 살펴보고 오겠다.
https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
힙 (자료 구조) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 1부터 100까지의 정수를 저장한 최대 힙의 예시. 모든 부모노드들이 그 자식노드들보다 큰 값을 가진다. 힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게
ko.wikipedia.org
힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조(tree-based structure)
최댓값과 최소값을 찾아내는 연산을 빠르게 하는 자료구조라고 하면 우선순위큐도 떠오른다.
그럼 힙과 우선순위 큐는 같은것인가 생각이 들 수 있다.
역시 우선순위 큐의 정의도 살펴보고 오겠다.
https://ko.wikipedia.org/wiki/%EC%9A%B0%EC%84%A0%EC%88%9C%EC%9C%84_%ED%81%90
우선순위 큐 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서, 우선순위 큐(Priority queue)는 평범한 큐나 스택과 비슷한 축약 자료형이다. 그러나 각 원소들은 우선순위를 갖고 있다. 우선순위 큐에서, 높은
ko.wikipedia.org
우선순위 큐가 힙이라는 것은 널리 알려진 오류이다.
우선순위 큐는 "리스트"나 "맵"과 같이 추상적인 개념이다.
마치 리스트는 연결 리스트나 배열로 구현될 수 있는 것과 같이,
우선순위 큐는 힙이나 다양한 다른 방법을 이용해 구현될 수 있다.
명시된 바와 같이 추상자료형인 우선순위 큐를 구현 하기 위해 힙을 사용하기도 한다 정도로 이해하고 넘어가면 될것이다.
그럼 다시 힙으로 돌아가서, 힙에 대해 더 알아보겠다.
힙은 부모,자식간의 키값에만 대소관계가 존재하고 형제 노드사이에서는 대소관계를 구분하지 않는다.
또 힙은 가장 높은 혹은 낮은 우선순위를 갖는 노드가 루트노드가 된다.
이런 특징을 갖는 힙은 다음과 같은 규칙을 갖는다.
루트 노드를 1번 정점이라고 한다면 그 자식 노드는 2번 정점, 3번 정점이 되고
2번 정점의 자식노드는 4번 정점, 5번 정점이된다.
즉 서로 대소관계를 갖는 부모노드의 관계는 부모노드가 n번 정점이라면
왼쪽 자식노드는 2*n 번 정점, 오른쪽 자식노드는 2*n + 1 번 정점이되는 규칙을 갖는다.
이는 역으로 생각하면 자식노드가 n번 정점이라면 부모노드는 n/2 번 정점이라는 것과 같은 의미이다.
이런 힙은 완전 이진트리의 구조이므로 힙의 시간복잡도는
$$O(log_2 n)$$ 을 갖는다.
왜냐하면 계층적 자료구조인 이진트리는 부모노드로부터 최대 2개의 자식노드를 갖기 때문에
점점 자식노드로 내려가다보면 n개의 데이터 삽입시 트리의 높이는
$$log_2 n$$
이 되기 때문이다.
이제 힙의 구성 과정을 살펴 보도록 하겠다.
힙의 구성과정은 다음과 같은 규칙을 따른다.
1. 현재 힙의 마지막노드에 값을 추가한다.
2. 값이 추가된 노드와 부모노드의 값을 비교후 우선순위에 있는 값을 부모노드로 교환한다.
간단한 예시를 들어 설명하자면 다음과 같은 배열로 최대 힙을 구성한다고 가정 해보겠다.
편의상 인덱스는 0번 부터가 아닌 1번 부터로 시작할것이다.
왼쪽부터 순서대로 데이터를 삽입하는 과정이다.
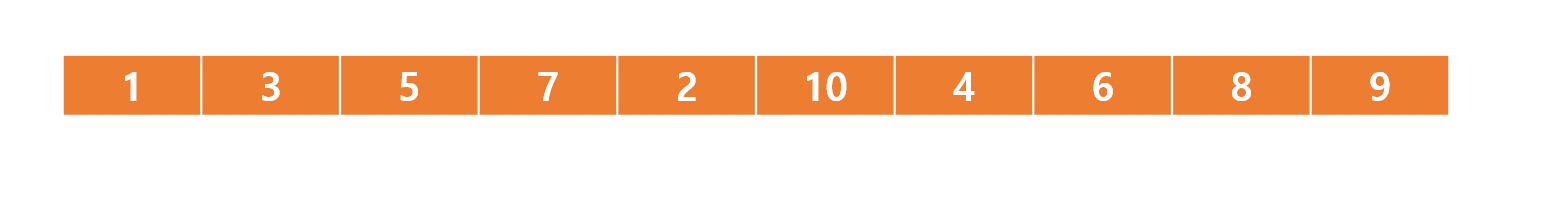
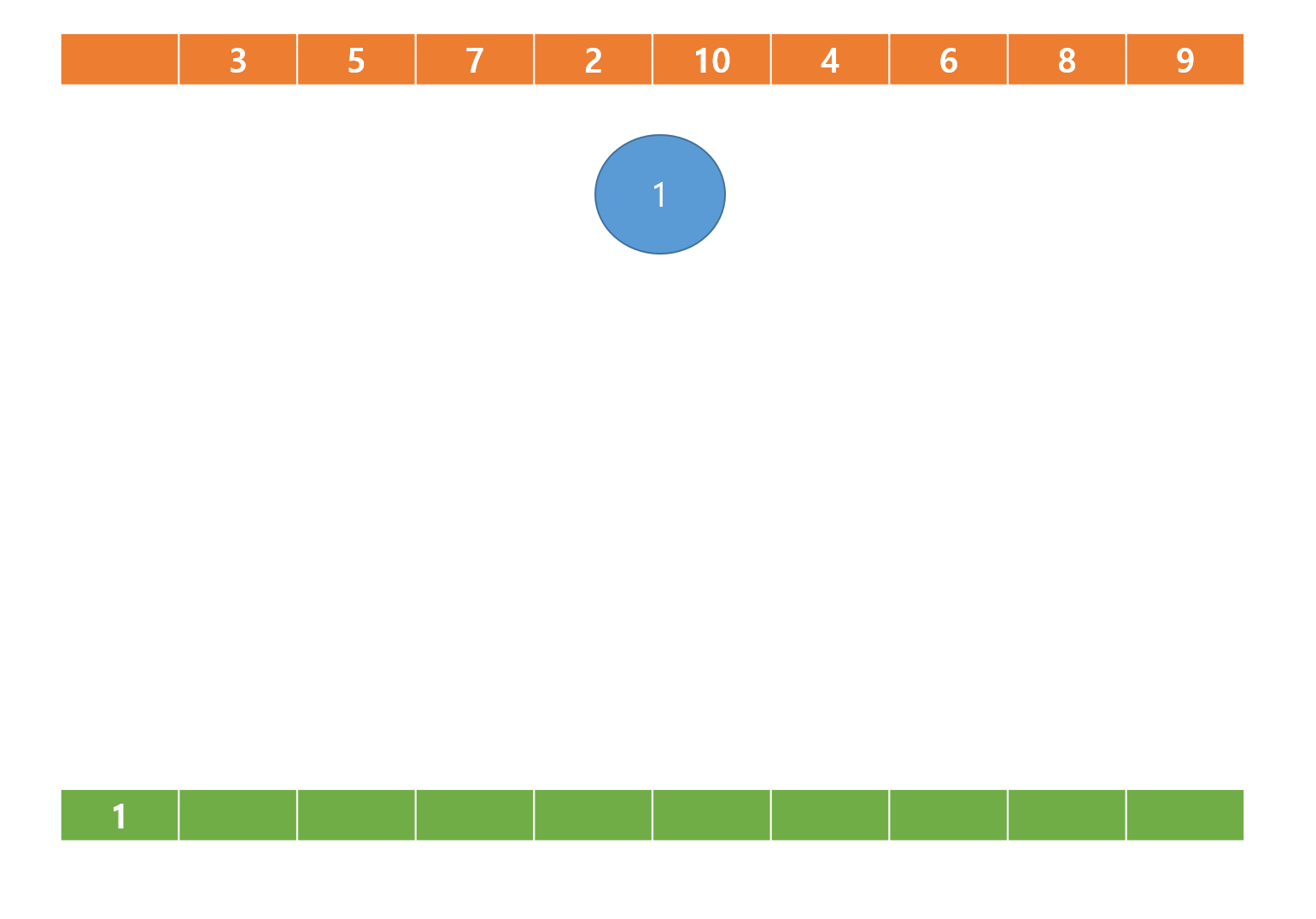
현재 힙의 마지막 노드는 1 이므로 배열의 첫번째 값이 1이 삽입되면
1번노드에 값이 추가되고, 1번 노드가 곧 루트노드 이므로 더이상 진행되지 않는다.
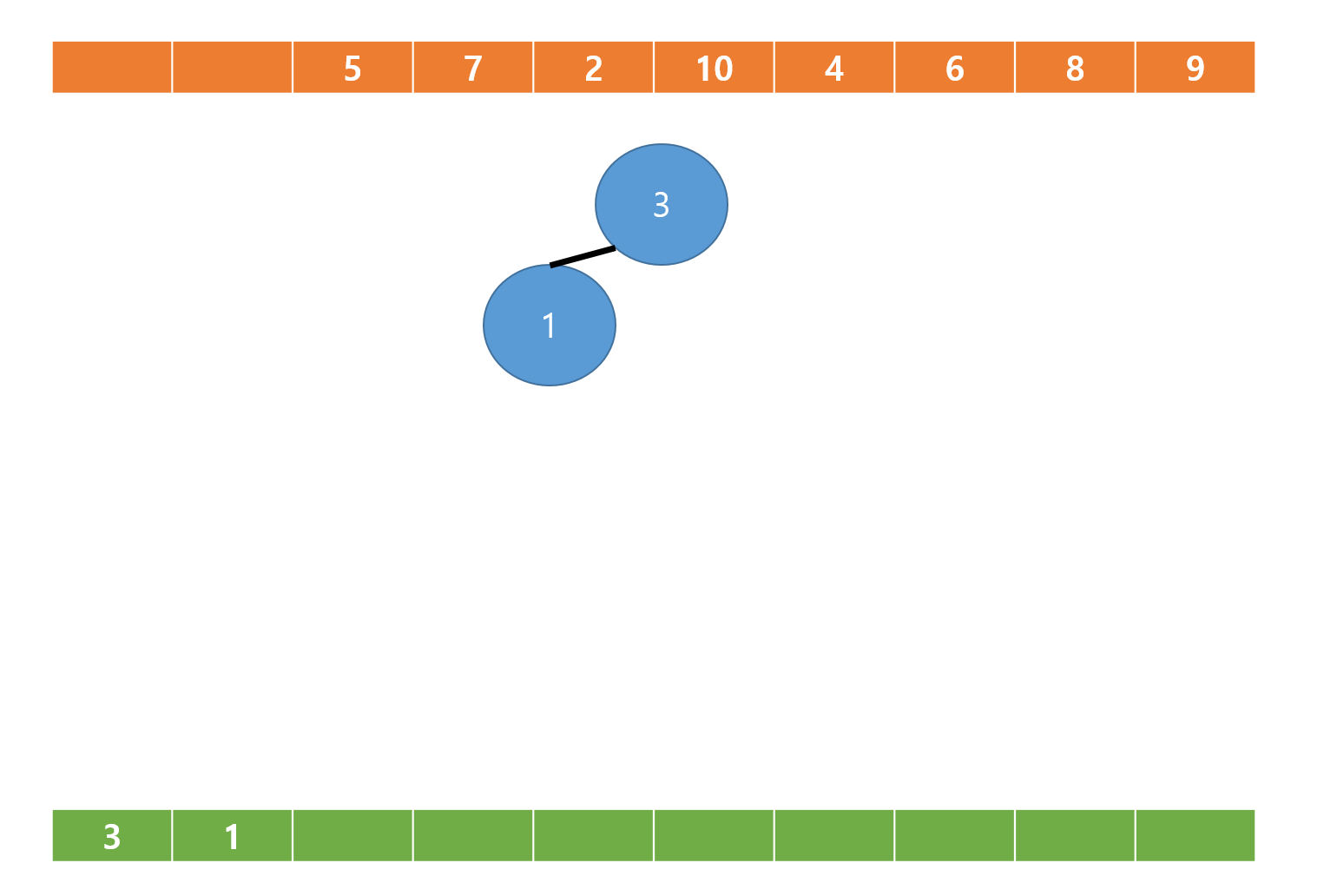
배열의 다음 값 2가 현재 힙의 마지막 노드인 2번 노드에 값이 추가되면,

위에서 언급한 규칙에 따라 현재노드인 2번 노드의 값 3과 부모노드인 1번 노드의 값 1과 비교 후
더 큰값을 갖는 3번 노드가 부모노드로 교환 된다.
배열의 다음값 5가 추가되면,

부모노드인 1번 노드와 현재 노드인 3번 노드를 비교 후 더 큰 값인 5가 부모노드로 교환된다.

배열의 다음값 7이 추가되면,
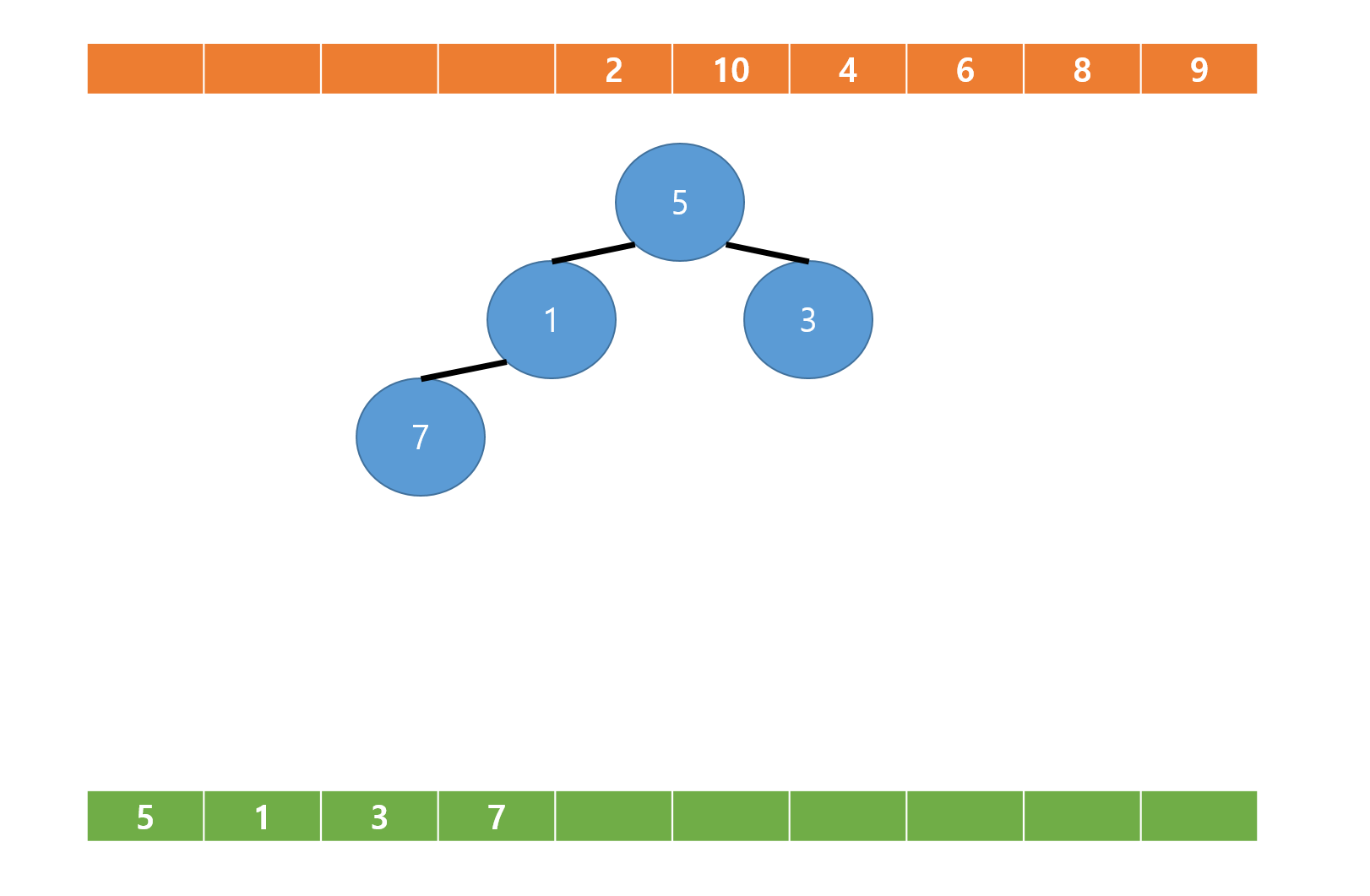
현재 노드인 4번노드와 그 부모노드인 2번 노드와 비교후 교환,
그리고 2번 노드와 그 부모노드인 1번 노드와 비교후 교환한다.

다음 배열의 값인 2가 현재 마지막 노드인 5번 노드에 추가되면, 이 경우 부모노드와 비교시 더 작으므로 교환되지 않는다.

이런 일련의 과정을 거쳐 힙이 구성되면 다음과 같은 모습을 갖게 된다.

앞서 말한 힙의 특징과 같이 부모 자식간의 키값에서 대소관계를 구분 하고
형제 노드간에는 대소관계를 구분하지 않는 모습을 갖는것을 볼 수 있다.
또 힙의 루트노드가 우선순위에 해당하는 값을 갖는것 역시 확인 할수 있다.
그렇다면 역으로 힙에서 데이터를 꺼내는 과정은 어떤식으로 진행되는지 확인해 보겠다.
그 과정은 다음과 같은 규칙을 따른다.
1. 루트노드의 값을 출력후 루트노드를 비운다.
2. 가장 마지막 노드를 루트노드와 교환후 마지막 노드를 삭제한다.
3. 부모자식 관계를 비교 후 우선순위에 있는 값을 부모노드로 교환한다.
그럼 앞서 구성한 힙에서 값을 꺼내는 과정을 한번 살펴보겠다.
먼저 루트노드의 값을 가져오고 루트노드를 비운다.

그리고 현재 마지막 노드인 10번 노드에 해당하는 값인 2를 루트노드와 교환후 10번 노드를 삭제한다.
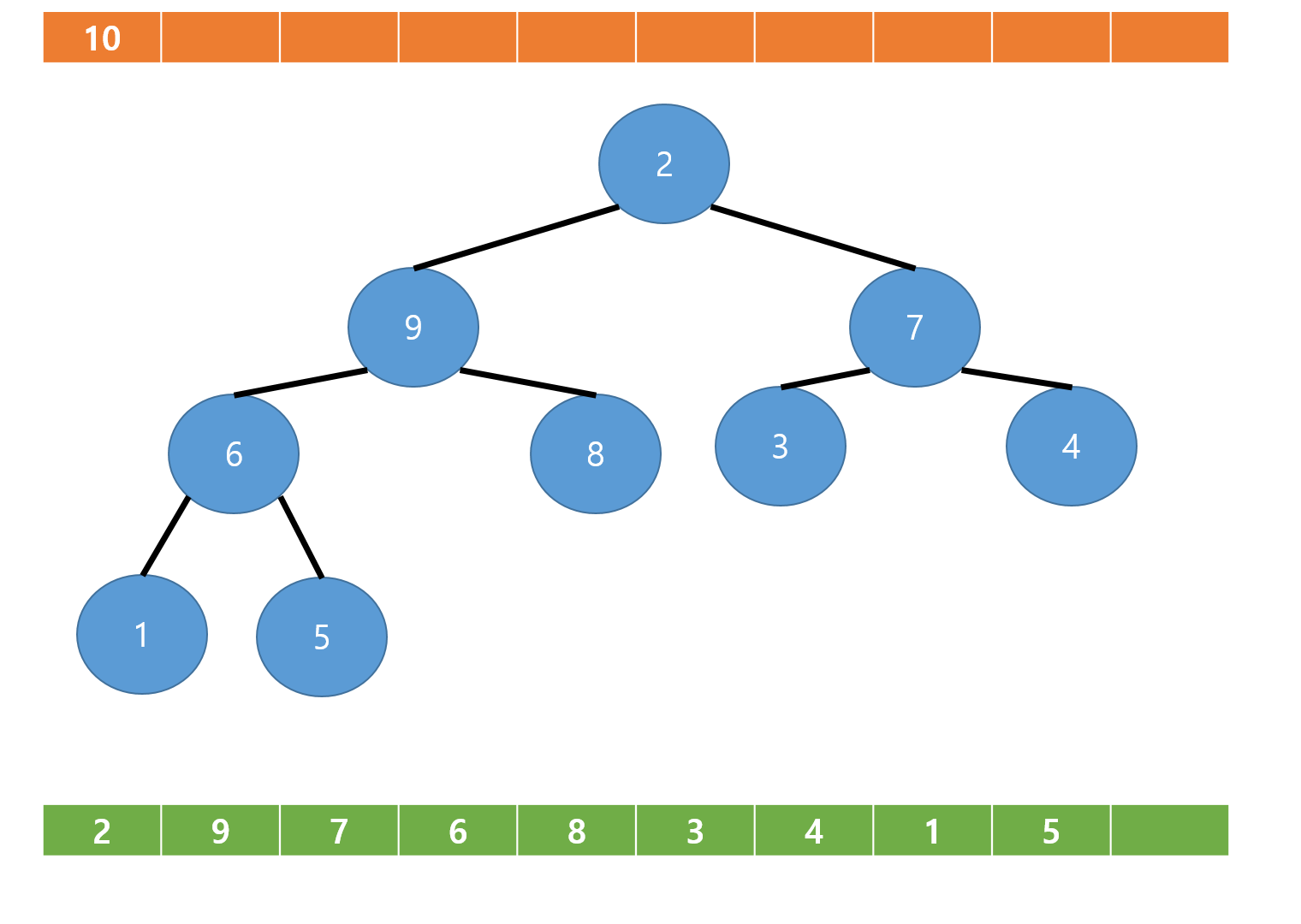
이제 루트부터 부모자식 관계를 비교후 교환하는 과정을 반복해준다.
이때 교환해야하는 상황이라면 형제노드끼리 비교해 좀 더 우선순위에 있는 노드와 교환한다.
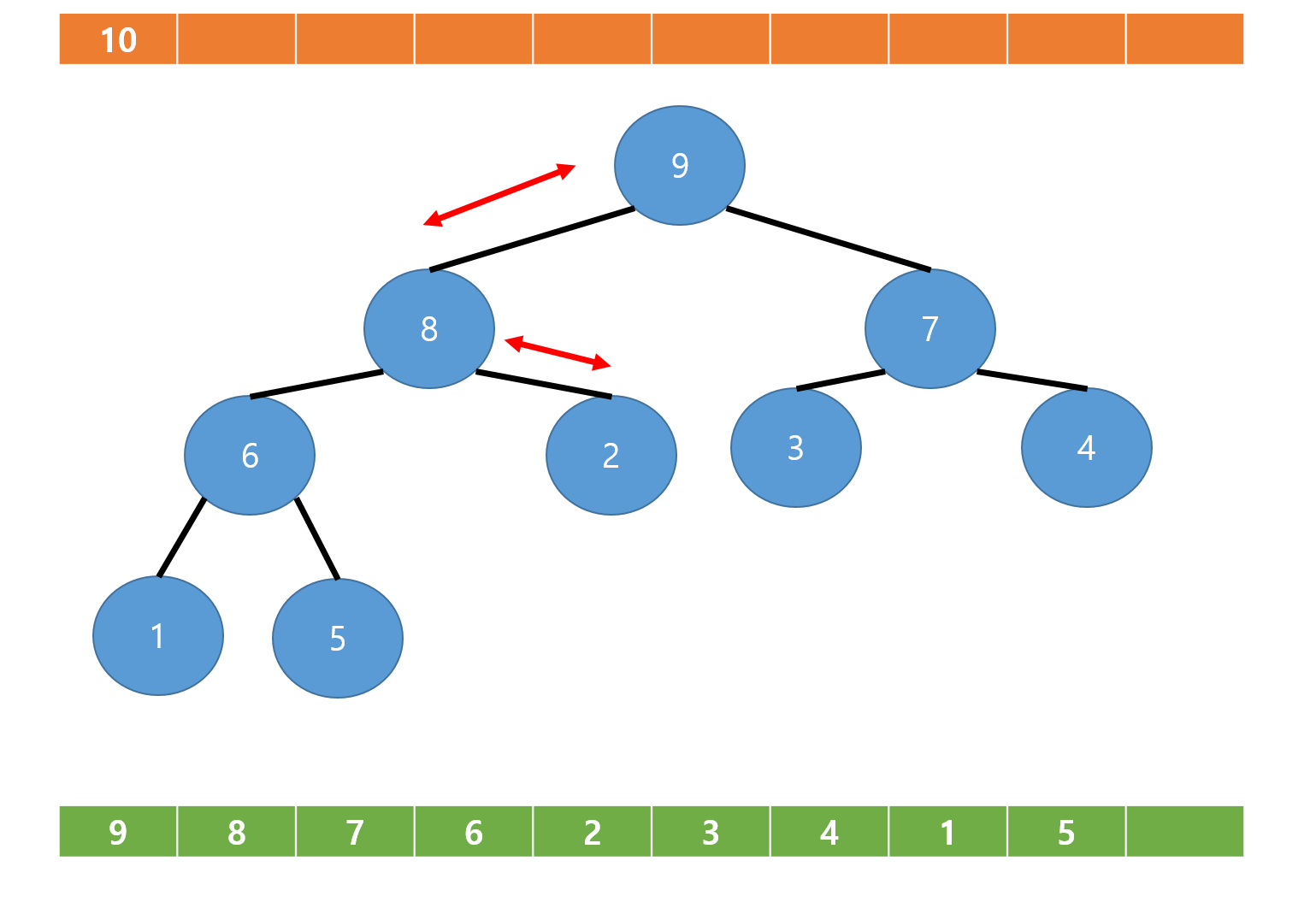
그림에서와 같이 부모노드인 1번 정점과 그 자식노드인 2번 , 3번 노드의 값을 비교 후 교환해야 하는 상황이라면,
2번 노드와 3번 노드의 값을 비교한다.
이때 2번 노드의 값이 더 우선순위에 있으므로 1번 노드와 2번 노드를 교환한다.
그리고 2번 노드와 4,5번 노드의 우선순위를 비교후 교환해야 하는 상황이므로,
4번 노드와 5번 노드중 더 우선순위인 5번 노드와 교환하는 것이다.
이러한 과정을 통해 힙에서 데이터를 가져오는 것이다.
역시 데이터를 꺼내고 힙을 다시 구성하는 것을 확인 할 수 있다.
또한 단순히 처음의 무작위 배열에서 최대값을 가져오는 연산을 수행한다 했을때,
힙을 사용하지 않는다면 1 ~ 10까지 순회하며 총 10번의 반복을 통해 비교 후 최대값을 가져오는 반면
힙을 사용한다면 현재 데이터의 경우 2번의 교환만을 통해 다시 힙을 구성하고 값을 가져오는 것을 확인 할 수 있다.
그렇다면 이제 코드로 구현해 보도록 하겠다.
먼저 모든 노드에 대해 인덱스로 관리해야 하므로 내부적으로 사용할 힙 배열을 하나 선언해주도록 하겠다.
이때 마지막 노드에 대해서도 관리해줄 변수도 하나 선언해준다.
생성자에서는 동적으로 힙의 크기를 입력받아 사용할 수 있도록 한다.
현재 힙에서 사용할 인덱스는 1부터 사용할것이므로 길이를 추가적으로 1늘려 선언해준다.
private Integer[] heap;
private int node,size;
HeapImpl(int n) {
this.size = n;
heap = new Integer[size + 1];
}
힙 구성시 값을 교환하는 경우가 빈번하게 일어나므로 값을 교환할 메소드를 하나 선언해준다.
private void exchange(int parentNode, int childNode) {
int temp = heap[childNode];
heap[childNode] = heap[parentNode];
heap[parentNode] = temp;
}
다음은 힙에 데이터를 추가하는 메소드이다.
위에서 언급한 규칙에 따라
1. 현재 힙의 마지막노드에 값을 추가한다.
2. 값이 추가된 노드와 부모노드의 값을 비교후 우선순위에 있는 값을 부모노드로 교환한다.
마지막 노드에 값을 추가해주고 비교해 값을 교환 해주도록 한다.
public void add(int data) {
heap[++node] = data;
for(int i = node; i > 1; i/=2) {
if(heap[i / 2] < heap[i]) {
exchange(i / 2, i);
}
}
}
마지막으로 힙의 데이터를 꺼내오는 메소드이다.
1. 루트노드의 값을 출력후 루트노드를 비운다.
2. 가장 마지막 노드를 루트노드와 교환후 마지막 노드를 삭제한다.
3. 부모자식 관계를 비교 후 우선순위에 있는 값을 부모노드로 교환한다.
역시 위에서 언급한 규칙에 따라 작성하되 주의할 것은
교환해야하는 상황이면 자식노드의 형제노드끼리 비교해서 교환해주고 현재 비교할 노드의 인덱스를
갱신해주어야 한다.
public int remove() {
int root = heap[1];
heap[1] = heap[node];
heap[node--] = null;
int nowNode = 1; // 루트부터 시작
while(nowNode * 2 < node) {
int left = nowNode * 2;
int right = nowNode * 2 + 1;
if(heap[nowNode] < heap[left] || heap[nowNode] < heap[right]) {
if(heap[left] >= heap[right]) {
exchange(nowNode,left);
nowNode = left;
}else {
exchange(nowNode,right);
nowNode = right;
}
}else {
break;
}
}
return root;
}
그리고 테스트를 위한 출력 메소드도 하나 생성 해주도록 하겠다.
public void prt() {
for(int i = 1; i <= size; i++) {
System.out.print(heap[i] + " ");
}
}
그럼 이전에 예시에서 다루었던 데이터를 삽입 시켜보고,
설명할때 예상했던 데이터로 구성이 되는지 확인하고
모든 힙의 데이터를 순차적으로 꺼내서 큰 순으로 가져오는지 확인 해보도록 하겠다.
public static void main(String[] args) {
HeapImpl heap = new HeapImpl(10);
int[] arr = {1,3,5,7,2,10,4,6,8,9};
for(int i = 0; i < 10; i++) {
heap.add(arr[i]);
}
heap.prt();
System.out.println();
for(int i = 0; i < 10; i++) {
System.out.print(heap.remove() + " ");
}
}
위와 같은 코드를 작성해 실행하면,

위에서 언급한 데이터와 동일하게 힙이 구성 되며
삭제시 우선순위에 맞게 힙이 재구성되어 출력되는것을 확인 할 수 있다.
아래는 코드의 전문이다.
package impl;
public class HeapImpl {
private Integer[] heap;
private int node,size;
HeapImpl(int n) {
this.size = n;
heap = new Integer[size + 1];
}
private void exchange(int parentNode, int childNode) {
int temp = heap[childNode];
heap[childNode] = heap[parentNode];
heap[parentNode] = temp;
}
public void add(int data) {
heap[++node] = data;
for(int i = node; i > 1; i/=2) {
if(heap[i / 2] < heap[i]) {
exchange(i / 2, i);
}
}
}
public int remove() {
int root = heap[1];
heap[1] = heap[node];
heap[node--] = null;
int nowNode = 1; // 루트부터 시작
while(nowNode * 2 < node) {
int left = nowNode * 2;
int right = nowNode * 2 + 1;
if(heap[nowNode] < heap[left] || heap[nowNode] < heap[right]) {
if(heap[left] >= heap[right]) {
exchange(nowNode,left);
nowNode = left;
}else {
exchange(nowNode,right);
nowNode = right;
}
}else {
break;
}
}
return root;
}
public void prt() {
for(int i = 1; i <= size; i++) {
System.out.print(heap[i] + " ");
}
}
}
위에서 언급했듯 힙은 정말 강력한 무기가 될 수 있는 자료구조이다.
지금은 예시를 10개 데이터만 넣어 사용했지만
가령 예를 들어 100000개의 데이터를 다룬다면,
$$log_2 100000 = 16.6XXX$$
이므로 100000번 연산하며 데이터를 탐색하는 과정에서
힙을 사용 한다면 최대 16회 정도 연산하면 데이터를 찾아 낼 수 있다.
힙을 사용하지 않고 최댓값 혹은 최솟값을 찾는 과정보다
힙을 사용한 과정이 정말 빠르게 이루어진다는것을 알 수 있다.
'알고리즘 > 구현' 카테고리의 다른 글
| [자료구조] 트라이(Trie)의 구현 (JAVA) (0) | 2023.10.05 |
|---|---|
| 에라토스테네스의 체 (JAVA) (0) | 2023.09.25 |
| 유클리드 호제법(JAVA) (0) | 2023.09.17 |
| [자료구조] 이진 트리와 순회의 구현(JAVA) (1) | 2023.09.16 |
| [자료구조] 큐(Queue)의 구현(JAVA) (0) | 2023.09.13 |
